Building a Scalable Analytics Architecture With Airflow and dbt (Part 1)

Editor's Note

At Astronomer, we're often asked how to integrate Apache Airflow® with specialized data tools that accommodate certain usage patterns. A tool that often comes up in conversation is dbt, an open-source library for analytics engineering that helps users build interdependent SQL models for in-warehouse data transformation.

Over the past few years, dbt has emerged as the standard for data engineers to write, organize, and run in-warehouse transformations. It's common to see teams use Airflow to orchestrate and execute dbt models within the context of a broader ELT pipeline that runs on Airflow and exists as a DAG.

In chatting with a handful of Astronomer customers who have spent time exploring solutions at the intersection of Airflow and dbt, we discovered that our friends at Updater have built a particularly great experience for authoring, scheduling, and deploying dbt models to their Airflow environment.

In this post, the first in a three-part series originally published in December 2020, John Lynch, Senior Data Engineer, and Flavien Bessede, Data Engineering Manager at Updater share the brilliant work they've done. This team has put extensive thought into building a scalable data architecture with both dbt and Airflow. In this series, they walk through the various approaches, considered limitations, and final output of a team.

All of the code in this post is available in this Github repository and can be run locally using the Astronomer CLI.

We hope you enjoy.

Note: Since this post was first published in 2020, Astronomer released two significant updates that significantly improve the experience of working with dbt and Airflow:

• Enhance Visibility with Cosmos: Released in July 2023 and now downloaded over 1 million times per month, Cosmos is an open-source provider package developed by Astronomer that represents your dbt projects as native Airflow tasks and DAGs, improving visibility and debugging. For those working with dbt Core, you can also orchestrate your jobs seamlessly using Airflow and Cosmos.
• Streamline Deployments with dbt deploys: In July 2024, we announced the availability of dbt deploys, a feature of our managed platform, Astro, enabling you to deploy your dbt projects to the same environment running your Airflow code. To streamline your dbt deployments, explore dbt on Astro

You can see a demo of these features in a 30-second tour.

Introduction

At Updater, we're big fans of Airflow (running on Astronomer of course) and dbt. Until recently, however, we've struggled to integrate the two in a way that accommodates all of our requirements; this doesn't just entail escaping Python dependency hell when trying to install dbt and Airflow in the same environment, but rather the more fundamental problem of figuring out the best way to have Airflow manage and schedule dbt runs at scale.

To understand the challenges associated with running dbt in the context of Airflow, we'll start from first principles with the dbt documentation. There, they have three primary suggestions outlining the ways to make dbt and Airflow play nicely together:

1. Use a community-contributed Airflow plugin to farm out execution to dbt Cloud.
2. Invoke dbt through a BashOperator.
3. Use pre-existing dbt Airflow operators in the community-contributed airflow-dbt python package.

All of these are perfectly reasonable methods that essentially unlock the same output: the ability to have Airflow call dbt and have dbt run your models for you.

Given that we wanted full control over our fundamental logic, we ended up going for Option 2. If you are just getting started with dbt and Airflow, invoking dbt through a BashOperator may not be conceptually clear. Once you have a handle on the basics, however, it's refreshingly simple; in Airflow, a task that invokes the BashOperator simply executes a shell command. Because the primary dbt interface is the command line, the BashOperator proves to be a useful tool to interact with the library; the familiar dbt run or dbt test commands can be executed directly in Airflow the same way they would be executed in any other shell.

A simple DAG that invokes these baseline commands with the BashOperator would look something like the following:

from datetime import timedelta

from airflow import DAG
from airflow.operators.bash_operator import BashOperator
from airflow.utils.dates import datetime
from airflow.utils.dates import timedelta

default_args = {
    'owner': 'astronomer',
    'depends_on_past': False,
    'start_date': datetime(2020, 12, 23),
    'email': ['noreply@astronomer.io'],
    'email_on_failure': False,
    'email_on_retry': False,
    'retries': 1,
    'retry_delay': timedelta(minutes=5)
}
dag = DAG(
    'dbt_dag',
    default_args=default_args,
    description='An Airflow DAG to invoke simple dbt commands',
    schedule_interval=timedelta(days=1),
)

dbt_run = BashOperator(
    task_id='dbt_run',
    bash_command='dbt run',
    dag=dag
)

dbt_test = BashOperator(
    task_id='dbt_test',
    bash_command='dbt test',
    dag=dag
)

dbt_run >> dbt_test

This Airflow DAG has two tasks:

1. A task that runs the dbt run command.
2. A subsequent task that runs dbt test.

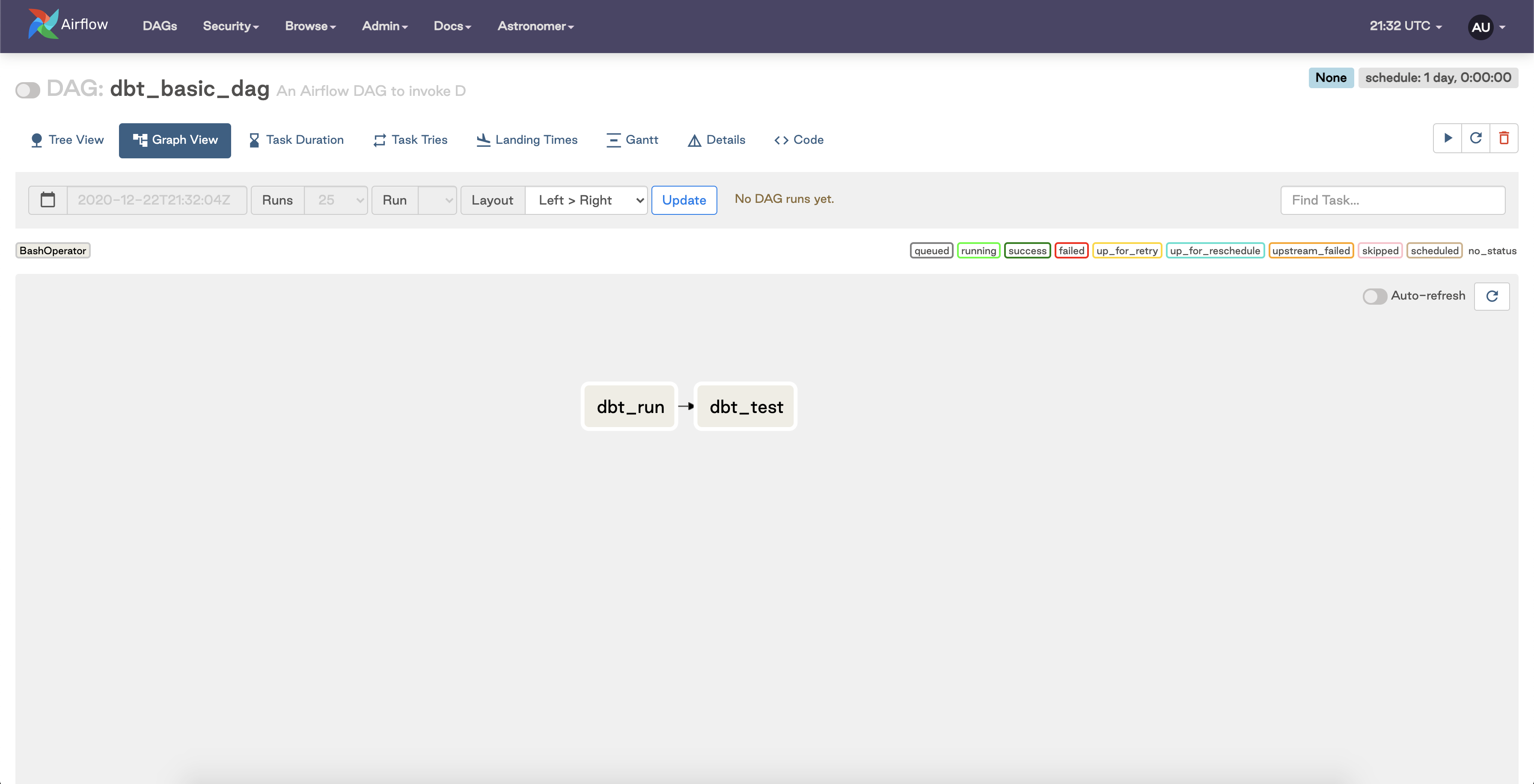
We end up with simple workflow that runs and tests a dbt model seamlessly. That is, until your dbt footprint scales and you need more granular control..

Scaling Challenges: Monolithic dbt Tasks in Airflow

When you're just getting started with a small dbt project, a model failure in Airflow isn't much of an issue and you can debug it the same way you'd handle troubleshooting any other Airflow: by taking a peek at your Airflow logs, determining the expected dbt model output, identifying the failing model, fixing it, deploying your new code, and then re-running your Airflow task to rebuild your dbt models. As your dbt project grows and you want to invoke an increasing number of models, however, things start to get complicated.

Imagine a case in which you would like to execute and test 50 dbt models on a daily basis using the DAG we defined above. As you monitor the status of your daily DAG (which now takes 2 hours to run because it needs to execute these 50 models) and hope for success , you get a dreaded Airflow task failure slack notification just as the DAG is about to finish running. You jump through the usual hoops of looking through Airflow logs and you notice that the final model in your workflow failed because you accidentally merged in some broken code. You fix the code and deploy it, but you soon realize that rerunning a single BashOperator Airflow task will not only rerun your broken model, but it will also rerun entire dbt project! And thus, you instead re-run your model and find yourself waiting for another two hours, praying for success once again.

As Airflow users may already know, the problem here is that Airflow doesn't know anything about your dbt DAG. As far as Airflow is concerned, the dbt run task is just some arbitrary shell command that happens to take a very long time to run. Moreover, Airflow best practices call for tasks to be atomic, meaning each task should be responsible for one operation that can be re-run independently of the others. Because this approach consolidates multiple dbt models into a single monolithic task, it limits the granular control users are accustomed to with their Airflow workloads in the context of dbt modeling.

Partial Solution: Breaking Down dbt DAGs, But...

A natural first step is to try to break down your monolithic dbt Airflow DAG into a collection of smaller DAGs that each run a subset of your dbt models. If you have a staging folder and a marts folder in your dbt project (as suggested in this wonderful article by the dbt folks) you could create two Airflow DAGs: one to run all of your staging models by calling dbt run --models staging via the BashOperator and another to run all of your marts models in the same way.

Once you've split up your dbt run commands into two separate DAGs, you'll need a way to make sure that all of your marts models run only after all of your staging models finish running. To set up interdependency between DAGs in Airflow, you can invoke a Sensor that waits for your first DAG to finish before it triggers the second.

This approach works decently well, but again it quickly breaks down at scale. The more models and Airflow DAGs you have to run, the more complicated it becomes to monitor and validate interdependent sensors. Soon enough, your team will begin relying on mental gymnastics to track dependencies between groups of models in each DAG. Moreover, the approach we're outlining here greatly undermines one of dbt's greatest strengths: model dependency management. dbt amazingly allows you to naturally define dependencies between models in code via a ref() function and then takes care of running everything in the right order under the hood. If we leverage the setup described above with multiple Airflow DAGs running their own subgroups of models, we inadvertently waste cycles worrying about the order of our tasks without taking advantage of core dbt functionality to alleviate that very problem.

The Ideal Solution: Mirroring the dbt DAG in Airflow

Given the barriers we encountered running dbt with Airflow at scale, we at Updater went back to the drawing board to consider more robust alternative solutions. After watching and participating in a few dbt talks, we determined that recreating the dbt DAG in Airflow might be a solution to all of our problems. If we create an individual Airflow task to run each and every dbt model, we would get the scheduling, retry logic, and dependency graph of an Airflow DAG with the transformative power of dbt.

Instead of having a single Airflow DAG that contains a single task to run a group of dbt models, we have an Airflow DAG run a single task for each model. This means that our entire dbt workflow is available at a much more granular level in the Airflow UI and, most importantly, we have fine-grained control of the success, failure, and retry of each dbt model as a corresponding Airflow task. If a model near the end of our dbt pipeline fails, we can simply fix the broken model and retry that individual task without having to rerun the entire workflow. Plus, we no longer have to worry about defining Sensors to configure interdependency between Airflow DAGs since we've consolidated our work into a single DAG.

In order to make this approach work, however, we had to dig into how dbt works under the hood. The starting point for us was a file that's generated by dbt and is called manifest.json. This file is generated in the target directory of your dbt project (see docs here) and contains a full representation of your dbt project, which gives you all the information you need to create your dbt Airflow DAG.

With this file in hand, the path to our desired experience becomes more clear:

1. Define a dbt DAG that reads and parses manifest.json .
2. Create a series of Airflow BashOperator tasks that run the appropriate run and test commands for a dbt model and use the information contained in manifest.json to set the correct dependencies between tasks.

Assuming that your manifest.json is available at dags/dbt/target/manifest.json in your Airflow project, the following DAG file will generate the dbt DAG on your behalf.

import datetime
import json

from airflow import DAG
from airflow.operators.bash_operator import BashOperator
from airflow.utils.dates import datetime
from airflow.utils.dates import timedelta

default_args = {
    'owner': 'astronomer',
    'depends_on_past': False,
    'start_date': datetime(2020, 12, 23),
    'email': ['noreply@astronomer.io'],
    'email_on_failure': False,
    'email_on_retry': False,
    'retries': 1,
    'retry_delay': timedelta(minutes=5)
}

dag = DAG(
    'dbt_dag',
    default_args=default_args,
    description='A dbt wrapper for airflow',
    schedule_interval=timedelta(days=1),
)

def load_manifest():
    local_filepath = "/usr/local/airflow/dags/dbt/target/manifest.json"
    with open(local_filepath) as f:
        data = json.load(f)

    return data

def make_dbt_task(node, dbt_verb):
    """Returns an Airflow operator either run and test an individual model"""
    DBT_DIR = "/usr/local/airflow/dags/dbt"
    GLOBAL_CLI_FLAGS = "--no-write-json"
    model = node.split["."](-1)

    if dbt_verb == "run":
        dbt_task = BashOperator(
            task_id=node,
            bash_command=f"""
            cd {DBT_DIR} &&
            dbt {GLOBAL_CLI_FLAGS} {dbt_verb} --target prod --models {model}
            """,
            dag=dag,
        )

    elif dbt_verb == "test":
        node_test = node.replace("model", "test")
        dbt_task = BashOperator(
            task_id=node_test,
            bash_command=f"""
            cd {DBT_DIR} &&
            dbt {GLOBAL_CLI_FLAGS} {dbt_verb} --target prod --models {model}
            """,
            dag=dag,
        )

    return dbt_task

data = load_manifest()

dbt_tasks = {}
for node in data["nodes"].keys():
    if node.split["."](0) == "model":
        node_test = node.replace("model", "test")

        dbt_tasks[node] = make_dbt_task(node, "run")
        dbt_tasks[node_test] = make_dbt_task(node, "test")

for node in data["nodes"].keys():
    if node.split["."](0) == "model":

        # Set dependency to run tests on a model after model runs finishes
        node_test = node.replace("model", "test")
        dbt_tasks[node] >> dbt_tasks[node_test]

        # Set all model -> model dependencies
        for upstream_node in data["nodes"][node]["depends_on"]["nodes"]:

            upstream_node_type = upstream_node.split(".")[0]
            if upstream_node_type == "model":
                dbt_tasks[upstream_node] >> dbt_tasks[node]

If you would like to try this DAG with your own dbt project in a local Airflow setup, clone the accompanying sample repo, add your own manifest file, and follow the steps in that repo to spin up a local Airflow environment with the Astro CLI.

This DAG definition reads the manifest.json file from local storage via the load_manifest() function and then loops through the nodes of the manifest file to create an Airflow task that either runs or tests a single dbt model. The final bit then loops through each node again, reads the dependencies from the manifest file for each node, and then sets the correct dependencies between the Airflow tasks (e.g. dbt_tasks[upstream_node] >> dbt_tasks[node]).

When running, this DAG will look something like this, pending what's in your manifest:

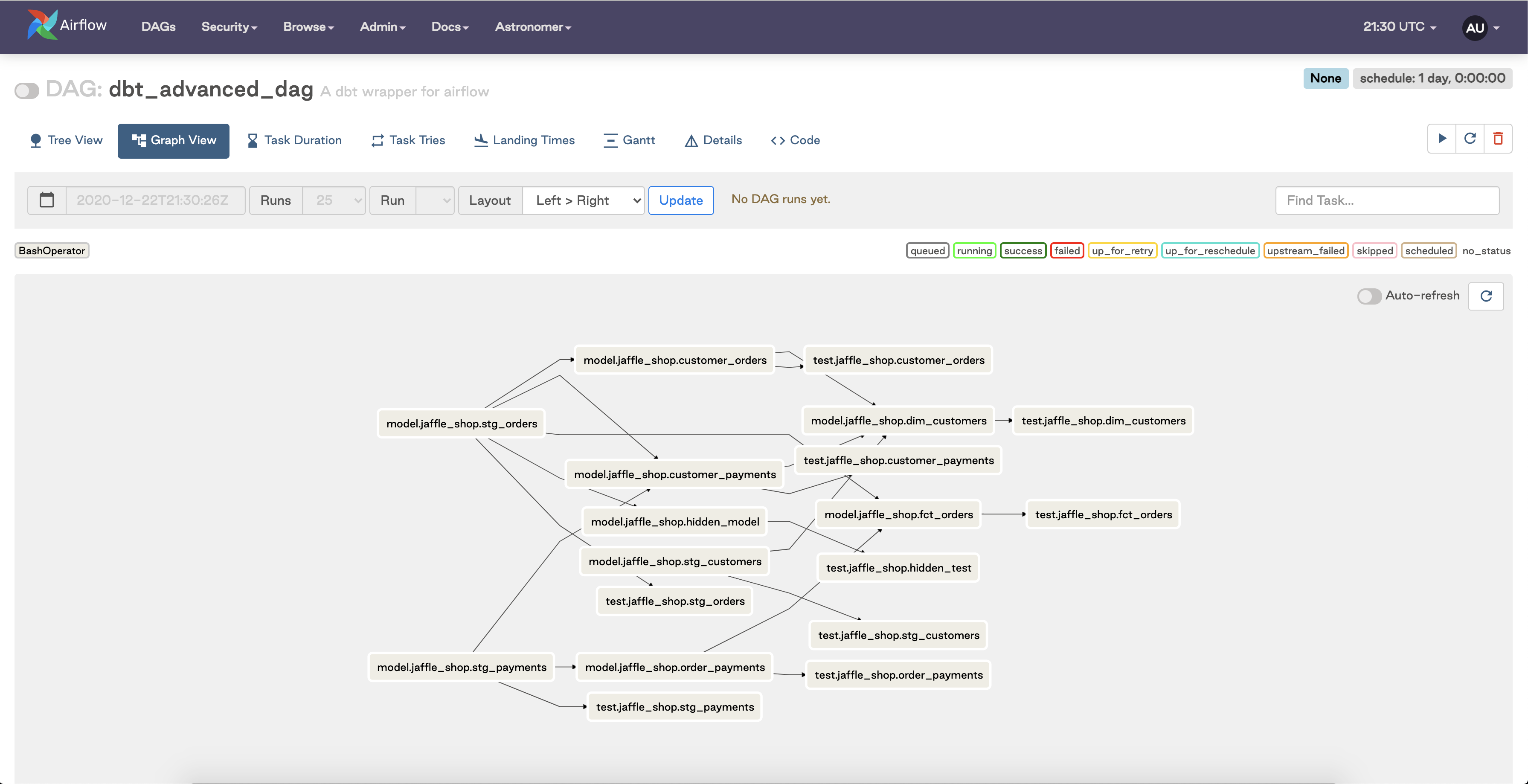
In short, this DAG file will read your manifest.json file, parse it, create the necessary BashOperator Airflow tasks, and then set the dependencies to match those of your dbt project. The end result is that each model in your dbt project maps to two tasks in your Airflow DAG — one task to run the model and another task to run the tests associated with that model. To top it all off, all of these models will run in the appropriate order thanks to the task dependencies we've set.

Looking Ahead

At this point, we have identified and built a great DAG authoring experience at the intersection of dbt and Airflow, but there are still a few outstanding questions:

• How do we productionize this approach and automate manual steps like the generation and deployment of our manifest.json file?
• How do we handle models that need to have different schedule intervals?
• How can we leverage our dbt transformation layer in the broader context of an ELT pipeline?

Go to the next part of this series to see us exploring answers to these questions and digging into a few creative ways to take this authoring experience into a production-ready setup.